OPERATING SYSTEM: Handling algorithm, excluding Banker's Algorithm

7.5.3 Banker's Algorithm

For resource categories that contain more than one instance the resource-allocation graph method does not work, and more complex ( and less efficient ) methods must be chosen.
The Banker's Algorithm gets its name because it is a method that bankers could use to assure that when they lend out resources they will still be able to satisfy all their clients. ( A banker won't loan out a little money to start building a house unless they are assured that they will later be able to loan out the rest of the money to finish the house. )
When a process starts up, it must state in advance the maximum allocation of resources it may request, up to the amount available on the system.
When a request is made, the scheduler determines whether granting the request would leave the system in a safe state. If not, then the process must wait until the request can be granted safely.
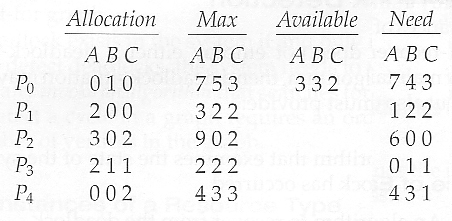
The banker's algorithm relies on several key data structures: ( where n is the number of processes and m is the number of resource categories. )
- Available[ m ] indicates how many resources are currently available of each type.
- Max[ n ][ m ] indicates the maximum demand of each process of each resource.
- Allocation[ n ][ m ] indicates the number of each resource category allocated to each process.
- Need[ n ][ m ] indicates the remaining resources needed of each type for each process. ( Note that Need[ i ][ j ] = Max[ i ][ j ] - Allocation[ i ][ j ] for all i, j. )
For simplification of discussions, we make the following notations / observations:
- One row of the Need vector, Need[ i ], can be treated as a vector corresponding to the needs of process i, and similarly for Allocation and Max.
- A vector X is considered to be <= a vector Y if X[ i ] <= Y[ i ] for all i.

7.5.3.1 Safety Algorithm

In order to apply the Banker's algorithm, we first need an algorithm for determining whether or not a particular state is safe.

This algorithm determines if the current state of a system is safe, according to the following steps:

Let Work and Finish be vectors of length m and n respectively.

Work is a working copy of the available resources, which will be modified during the analysis.

Finish is a vector of booleans indicating whether a particular process can finish. ( or has finished so far in the analysis. )

Initialize Work to Available, and Finish to false for all elements.

Find an i such that both (A) Finish[ i ] == false, and (B) Need[ i ] < Work. This process has not finished, but could with the given available working set. If no such i exists, go to step 4.

Set Work = Work + Allocation[ i ], and set Finish[ i ] to true. This corresponds to process i finishing up and releasing its resources back into the work pool. Then loop back to step 2.

If finish[ i ] == true for all i, then the state is a safe state, because a safe sequence has been found.

( JTB's Modification:

In step 1. instead of making Finish an array of booleans initialized to false, make it an array of ints initialized to 0. Also initialize an int s = 0 as a step counter.

In step 2, look for Finish[ i ] == 0.

In step 3, set Finish[ i ] to ++s. S is counting the number of finished processes.

For step 4, the test can be either Finish[ i ] > 0 for all i, or s >= n. The benefit of this method is that if a safe state exists, then Finish[ ] indicates one safe sequence ( of possibly many. ) )

7.5.3.2 Resource-Request Algorithm ( The Bankers Algorithm )

Now that we have a tool for determining if a particular state is safe or not, we are now ready to look at the Banker's algorithm itself.

This algorithm determines if a new request is safe, and grants it only if it is safe to do so.

When a request is made ( that does not exceed currently available resources ), pretend it has been granted, and then see if the resulting state is a safe one. If so, grant the request, and if not, deny the request, as follows:

Let Request[ n ][ m ] indicate the number of resources of each type currently requested by processes. If Request[ i ] > Need[ i ] for any process i, raise an error condition.

If Request[ i ] > Available for any process i, then that process must wait for resources to become available. Otherwise the process can continue to step 3.

Check to see if the request can be granted safely, by pretending it has been granted and then seeing if the resulting state is safe. If so, grant the request, and if not, then the process must wait until its request can be granted safely.The procedure for granting a request ( or pretending to for testing purposes ) is:

Available = Available - Request

Allocation = Allocation + Request

Need = Need - Request

7.5.3.3 An Illustrative Example

Consider the following situation:

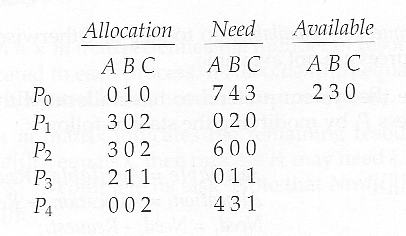
And now consider what happens if process P1 requests 1 instance of A and 2 instances of C. ( Request[ 1 ] = ( 1, 0, 2 ) )

What about requests of ( 3, 3,0 ) by P4? or ( 0, 2, 0 ) by P0? Can these be safely granted? Why or why not?